Usage

The Documentation of the functions provides in detail in the API Documentation (mcfit.github.io/pyemcee/doc). This Python library creates the MCMC sampling for given upper and lower uncertainties, and propagates uncertainties of parameters into the function

You need to define your function. For example:

def myfunc21(input1):
   result1 = np.sum(input1)
   result2 = input1[1] ** input1[0]
   return [result1, result2]

and use the appropriate confidence level and uncertainty distribution. For example, for a 1.645-sigma standard deviation with a uniform distribution:

clevel=.9 # 1.645-sigma
use_gaussian=0 # uniform distribution from min value to max value

for a 1-sigma standard deviation with a Gaussian distribution:

clevel=0.68268949 # 1.0-sigma
use_gaussian=1 # gaussian distribution from min value to max value

and specify the number of walkers and the number of iterations:

walk_num=30
iteration_num=100

Now you provide the given upper and lower uncertainties of the input parameters:

input1 = np.array([1., 2.])
input1_err = np.array([0.2, 0.5])
input1_err_p = input1_err
input1_err_m = -input1_err
output1 = myfunc21(input1)
output1_num = len(output1)

You should load the pyemcee library class as follows:

import pyemcee
import numpy as np

You can then create the MCMC sample and propagate the uncertainties of the input parameters into your defined functions as follows:

mcmc_sim = pyemcee.hammer(myfunc21, input1, input1_err_m,
                          input1_err_p, output1, walk_num,
                          iteration_num, use_gaussian)

To determine the upper and lower errors of the function outputs, you need to run:

output1_error = pyemcee.find_errors(output1, mcmc_sim, clevel, do_plot=1)

which shows the following distribution histograms:

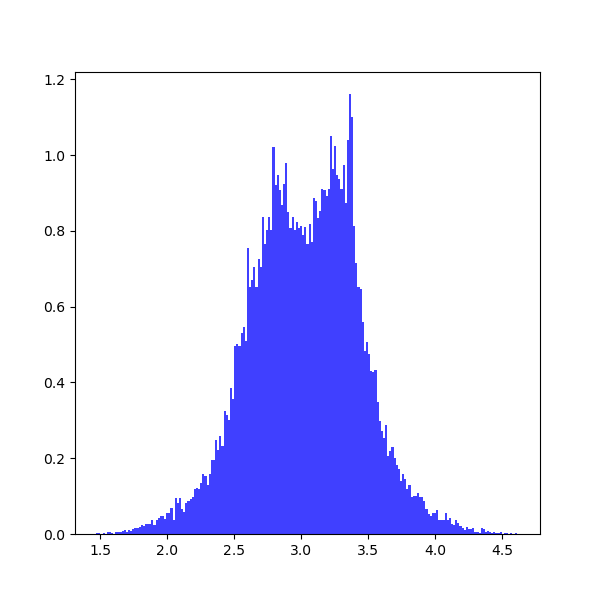
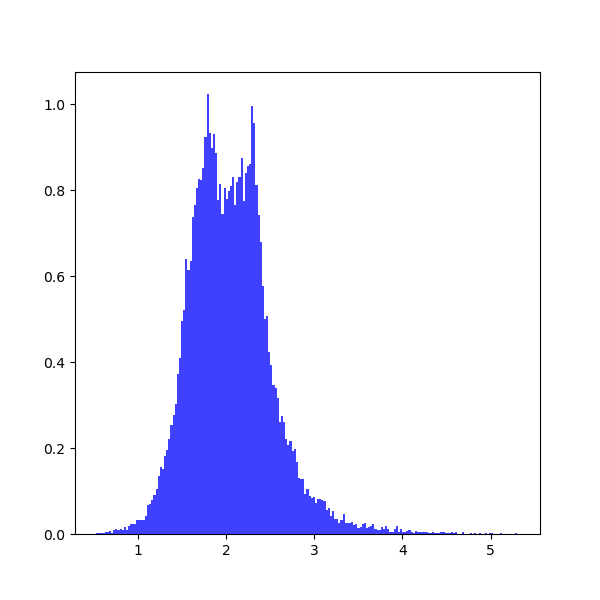
To print the results:

for i in range(0, output1_num):
   print(output1[i], output1_error[i,:])

which provide the upper and lower limits on each parameter:

3.0 [-0.35801017 0.35998471]
2.0 [-0.37573196 0.36297235]

For other standard deviation, you should use different confidence levels:

clevel=0.38292492 # 0.5-sigma
clevel=0.68268949 # 1.0-sigma
clevel=0.86638560 # 1.5-sigma
clevel=0.90       # 1.645-sigma
clevel=0.95       # 1.960-sigma
clevel=0.95449974 # 2.0-sigma
clevel=0.98758067 # 2.5-sigma
clevel=0.99       # 2.575-sigma
clevel=0.99730020 # 3.0-sigma
clevel=0.99953474 # 3.5-sigma
clevel=0.99993666 # 4.0-sigma
clevel=0.99999320 # 4.5-sigma
clevel=0.99999943 # 5.0-sigma
clevel=0.99999996 # 5.5-sigma
clevel=0.999999998# 6.0-sigma